增益模型（Uplift）

增益模型定义：一种用于估算个体干预增量( uplift )的模型，即 干预动作(treatment) 对 用户响应行为(outcome) 产生的效果。

因果推断的应用，主要是 Uplift 建模，即增量预估

为什么要使用 Uplift 模型

用一个简单的例子来介绍此模型。假设我们是个电商平台，一件标价300元的商品，用户的购买率为6%。现有一批预算可以给用户发放10元的优惠券以提升用户购买率。需要给每个用户都发放优惠券吗？答案显然是否定，那么这批优惠券应该发送给平台的哪些用户呢？

此时我们脑海中有四类用户：

Persuadables：不发送优惠券则不买，发送优惠券则购买；
Sure things：不论是否发送优惠券均会购买；
Lost causes: 不论是否发送优惠券均不会购买；
Sleeping Dogs: 不发送优惠券会购买，发送优惠券反而不买；

左上的 Persuadables(说服型) 类用户被发券后产生了正向变化，从不买转化为购买，干预后购买率得以提升，此部分是我们真正想要进行触达干预的营销敏感用户。

而右上的 Sure things(确认型)类 用户以及左下的 Lost causes(沉睡型) 用户无论是否发券均不会改变其原本的购买行为，对这部分用户发送优惠券则会造成资源浪费。

右下的Sleeping Dogs(勿扰型) 用户对营销可能相对反感，干预会产生反效果，这类用户我们尽量避免打扰。

Uplift模型要解决的问题就是通过建模预测的方法精准的去对这四类用户进行分群！

因为我们获取到的训练训练数据是不完整的，对于单个用户来说，不可能同时观测到在有干预(发券)和没有干预(不发券)两种情况下的表现，这也是因果推断中的反事实的问题。

什么时间用，怎么用

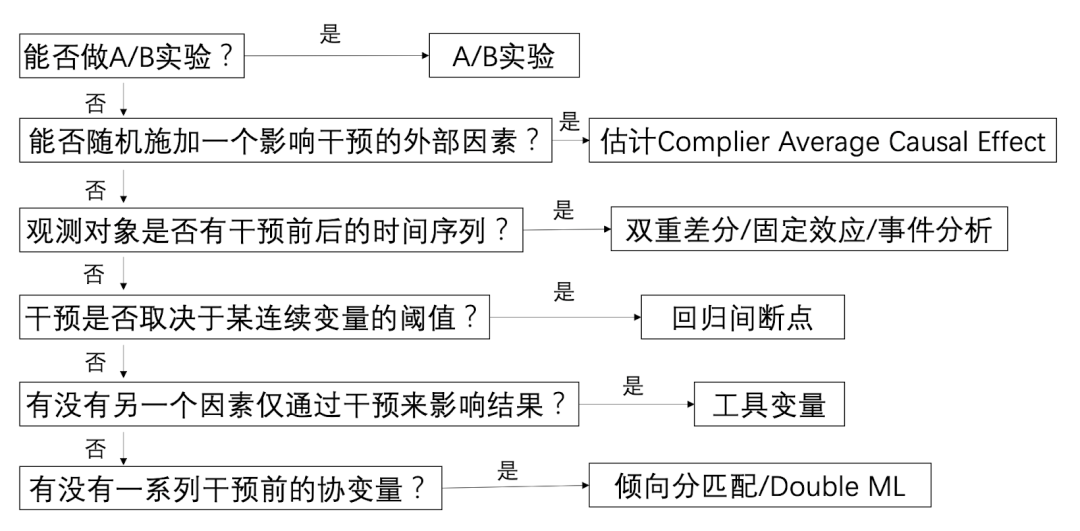
条件允许的情况下，ab test是最佳的因果推断方法之一。但ab test也有自己的局限性：

AB test不可进行：比如我们不能强迫一组用户‘吸烟’，另一组用户‘不吸烟’去观察吸烟对健康的危害；
AB test成本太高：当线上实验的选择太多，而产品的流量/时间成本是有限时，逐一对每一个实验都进行测试显然不现实，此时通过离线数据进行因果推断可以帮助我们科学地预判不同实验策略的‘前途’，让我们可以优先尝试前途更加光明的实验；

因果推断是通过特定的方法对观察性数据控制混杂变量以拟合随机试验。所有的方法的核心思想，都离不开控制混杂（control confounding variables）

在上文小明高考的例子里，我提到过要寻找一模一样的小明2号，而一模一样的目的就是为了控制混杂变量。只有在控制了两者混杂变量一致，仅有高考分数不同的情况下，我们才能计算高考分数对工资收入的影响。

混杂变量是指对于因和果都有影响的因素，忽视它们会对结果带来致命的偏倚；对小明和小明2号来说，需要控制的混杂变量有：上过的学校，遇见过的老师，自己的学习、睡眠时长，等等等等，因为这些都会影响高考的分数（因），也会影响未来的收入（果）。但是例如小明的头发颜色、身高这种特征并不会对于因果变量有什么影响，无需控制。

所以在实践中很关键的一点，就是判断到底需要控制哪些混杂，才能让你认为小明和小明2号是同质的。判断混杂因子并没有一个标准方法，而是需要结合对业务的深度理解。不同的数据类型、场景会有不同的适用方法，下面是一些常见的判断标准和对应方法：

常见方法

模型

模型说明

假设有 $N$ 个用户， $Y_i(1)$ 表示我们对用户 $i$ 干预后的结果，比如给用户 $i$ 发放优惠券后（干预）用户下单（结果）， $Y_i(0)$ 表示没有对用户干预的情况下用户的输出结果，比如没有给用户 $i$ 发放优惠券（干预），用户下单（结果）。用户 $i$ 的因果效应 (causal effect）的计算如下：

\tau_i=Y_i(1)-Y_i(0) \tag{1}

增益模型的目标就是最大化 $\tau_i$ ，这是一个增量，即有干预策略相对于无干预策略的提升，简单讲就是干预前后结果的差值。实际使用时会取所有用户的因果效应期望的估计值来衡量整个用户群的效果，称为条件平均因果效应 CATE (Conditional Average Treatment Effect)

CATE=\tau(X_i)=E[Y_i(1)|X_i]-E[Y_i(0)|X_i] \tag{2}

上式中 $X_i$ 是用户 $i$ 的特征，所谓的 conditional 指基于用户特征。

(2)式是理想的 uplift 计算形式，实际上，对用户 $i$ 我们不可能同时观察到使用策略和未使用策略的输出结果，即不可能同时得到 $Y_i(1)$ 和 $Y_i(0)$ 。因为对某个用户，我们要么发优惠券，要么不发。

因此将(2)式修改一下：

Y^{OBS}_i=W_iY_i(1)+(1-W)Y_i(0) \tag{3}

其中 $Y_i^{OBS}$ 是用户 $i$ 可以观测到的结果， $W_i$ 是一个二值变量，如果对用户 $i$ 使用了策略，那么 $W_i=1$ ，否则 $W_i=0$ 。

在条件独立的假设下，条件平均因果效应的期望估计值是：

\tau(X_i)=E[Y_i^{OBS}|X_i=x,W=1]-E[Y_i^{OBS}|X_i=x,W=0] \tag{4}

上式要满足条件独立(CIA)条件，即用户特征与干预策略是相互独立的

{Y_i(1),Y_i(0)} \perp W_i|X_i \tag{5}

实践上，满足CIA这样条件的样本的可以通过AB实验获取，因为时随机实验，可以保证用户（特征）与干预策略是相互独立的。

增益模型要优化 $\tau(X_i)$ ，值越高越好。然而一个用户不能同时观察到使用干预策略和不使用干预策略的结果，因此 $\tau(X_i)$ 是难以直接优化的。但如果通过AB实验，可以获得使用干预策略和不使用干预策略两组人群，如果两组人群的特征分布一致，可以通过模拟两组人群的 $\tau(X_i)$ 得到个体用户的 $\tau(X_i)$ 。因此增益模型依赖AB实验的数据。

下面介绍三种增益模型建模方法。

Uplift Model 常用建模方法

T-Learner，其中T代表two的意思，也即用两个模型。它的主要思想是对干预数据和无干预数据分别进行建模，预估时数据进入两个模型，用两个模型的预测结果做差值，来得到预估的增量。该方法的优点是原理比较简单直观，可以快速实现。但缺点是，因为两个模型的精度不一定非常高，所以两个模型的误差会有叠加，并且因为有差分的操作，这是间接计算的增量。

S-Learner，其中S代表single，也即用一个模型。它的主要思想是把干预作为特征输入模型，在预测时，同样是用有干预的结果和无干预的结果做差，得到预估增量。和Response模型比较像，就相当于特征里面有“是否干预”这样的特征，它的优点是，相比T-Learner减少了误差的累积，但缺点同样是间接的计算增量。

X-Learner，它的思想是先分别对有干预、无干预数据进行建模，再用两个模型来交叉预测，得到干预数据和无干预数据分别的反事实结果。因为这是训练数据，它是有真实label的，再用真实label和刚才预测的反事实结果做差，得到增量；把增量再作为label，再针对增量进行建模。同时对有无干预进行建模，得到干预的倾向分，并在预测增量的时候引入倾向分权重。方法的优点在于，可以对前面我们预测出来的增量建模时加入先验知识进行优化，来提高预测的准确性，另外还引入了倾向分权重来减少预测的误差。但它的缺点也是多模型的误差，可能会有累积，并且归根结底也是间接得到预测增量。

上面这几种方法都是间接得到预测增量，当然，也有直接对增量进行建模的方法，比如基于决策树的模型Tree-based Model。近几年也有一些深度学习的方法，比如DragonNet

评估

难点：不存在 ground truth ，因为无法同时对一个样本干预和不干预。

因为上述难点，大部分衡量指标需要通过聚合指标（衡量群体）实现，例如uplift bins和uplift curves.

uplift bins

一种常见做法如下：

对所有样本（包括实验组和对照组）同时预测uplift值
按照uplift值排序，计分别算每个十分位里实验组和对照组的outcome平均值
计算每个十分位两组平均值的差

通过以上的方式获得了每个十分位干预后outcome值的增量。

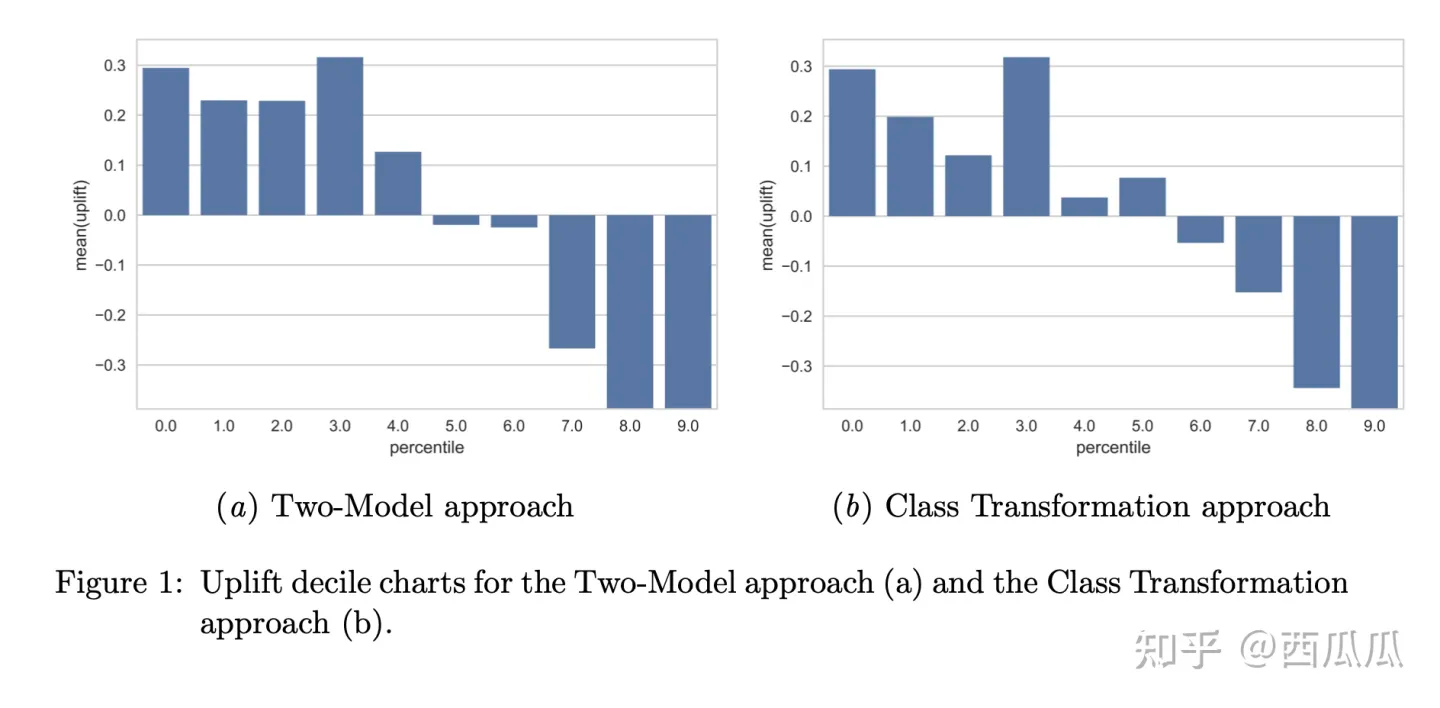
上图存在问题：无法比较两个不同模型的好坏

cumulative decile charts

为了能跨模型比较，我们引入累积增益图：第一个bar代表前10%的uplift，第二个bar代表前20%的uplift。一个表现好的模型在前半段会有比较大的值，后半段下降。

Cumulative Gain：计算uplift值乘以每个bin的总人数（图2(b)）

$\left(\frac{Y^{T}}{N^{T}}-\frac{Y^{C}}{N^{C}}\right)\left(N^{T}+N^{C}\right)$ 其中 $Y^T$ 和 $N^T$ 分别代表实验组中响应的总人数和实验组的总人数，对照组同理。

图2(b)对运营的同学很有用：如果希望圈选一部分人进行干预，可以通过图找到增益效果的最大值（例：圈选前40%的用户可以达到最大值）

AUUC

以上都是通过可视化的形式展示模型好坏，这里引入数值指标用于直接比较。

我们可以通过以下公式（uplift curves）计算测试集上每一个 t 的增益效果

f(t)=\left(\frac{Y_{t}^{T}}{N_{t}^{T}}-\frac{Y_{t}^{C}}{N_{t}^{C}}\right)\left(N_{t}^{T}\,+\,N_{t}^{C}\right)

其中 $t$ 表示按预测 uplift 值进行排序的前 $t$ 个观察值

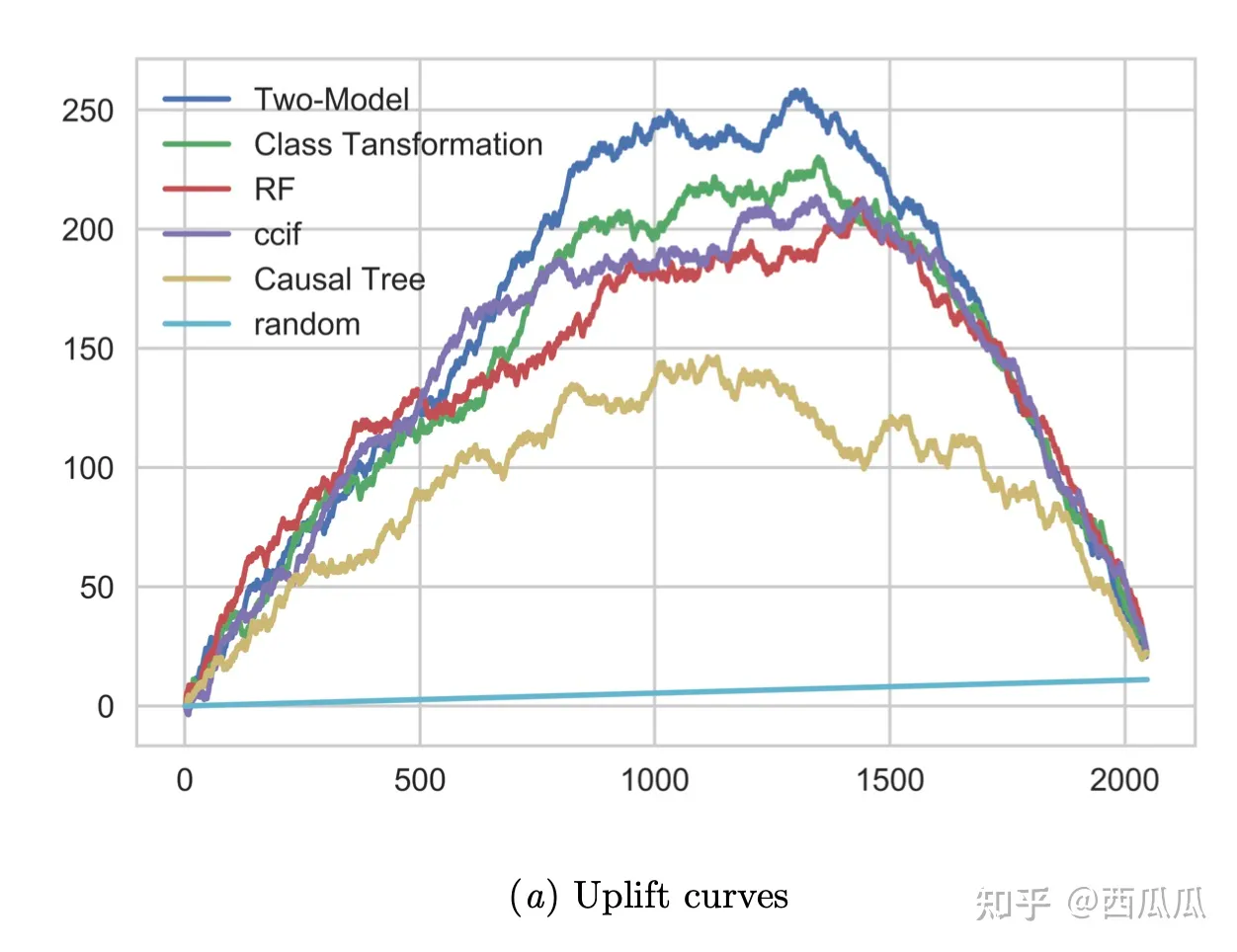
基于上图，我们可以得到 uplift model 最常用的评估指标AUUC(Area Under Uplift Curve)，即曲线下的面积。

Qini Curve

另外一种相似的Qini Curve表示如下，将Qini系数定义为曲线下的面积 $g(t)=Y_{t}^{T}-\frac{Y_{t}^{C}N_{t}^{T}}{N_{t}^{C}}$

可以看到 qini curve 与 uplift curve 的关系如下（平衡情况下系数为2）：

$f(t)=\frac{g(t)\left(N_{t}^{T}+N_{t}^{C}\right)}{N_{t}^{T}}$ 通常情况下，Uplift Curve 会受实验对照组样本数比例影响，Qini Curve 更稳定一些。

增益模型（Uplift）

为什么要使用 Uplift 模型

什么时间用，怎么用

模型