Confusion Matrix
混淆矩阵,是计算后面进一步评估模型的其他指标(TPR、FPR、AUC、ROC等)的第一步
当然,混淆矩阵如果说要明白,确实很简单,无非就是把模型预测的结果,进行分类统计罢了。
但是,xxx
TP、TN、FP、FN
让我们从一个风控领域常见的反欺诈模型开始,期望是识别哪些交易是有欺诈风险的
在我们训练完模型之后,就可以使用模型对现有的样本进行预测
当然每个样本的真实标签我们也有,这就可以对每一个样本的预测进行校验

很明显,我们的模型会在某些样本上判断错误,为了进一步统计这些错误,我们可以对错误类型进行分类。
一共有两种类型的错误
- 第一种是【错误的预警】:将实际为普通的交易判定成为了欺诈交易
- 第二种是【漏报】:将实际为欺诈的交易判定成了普通的交易
上面的第一种错误,就称为 False Positive,第二种就称为 False Negative
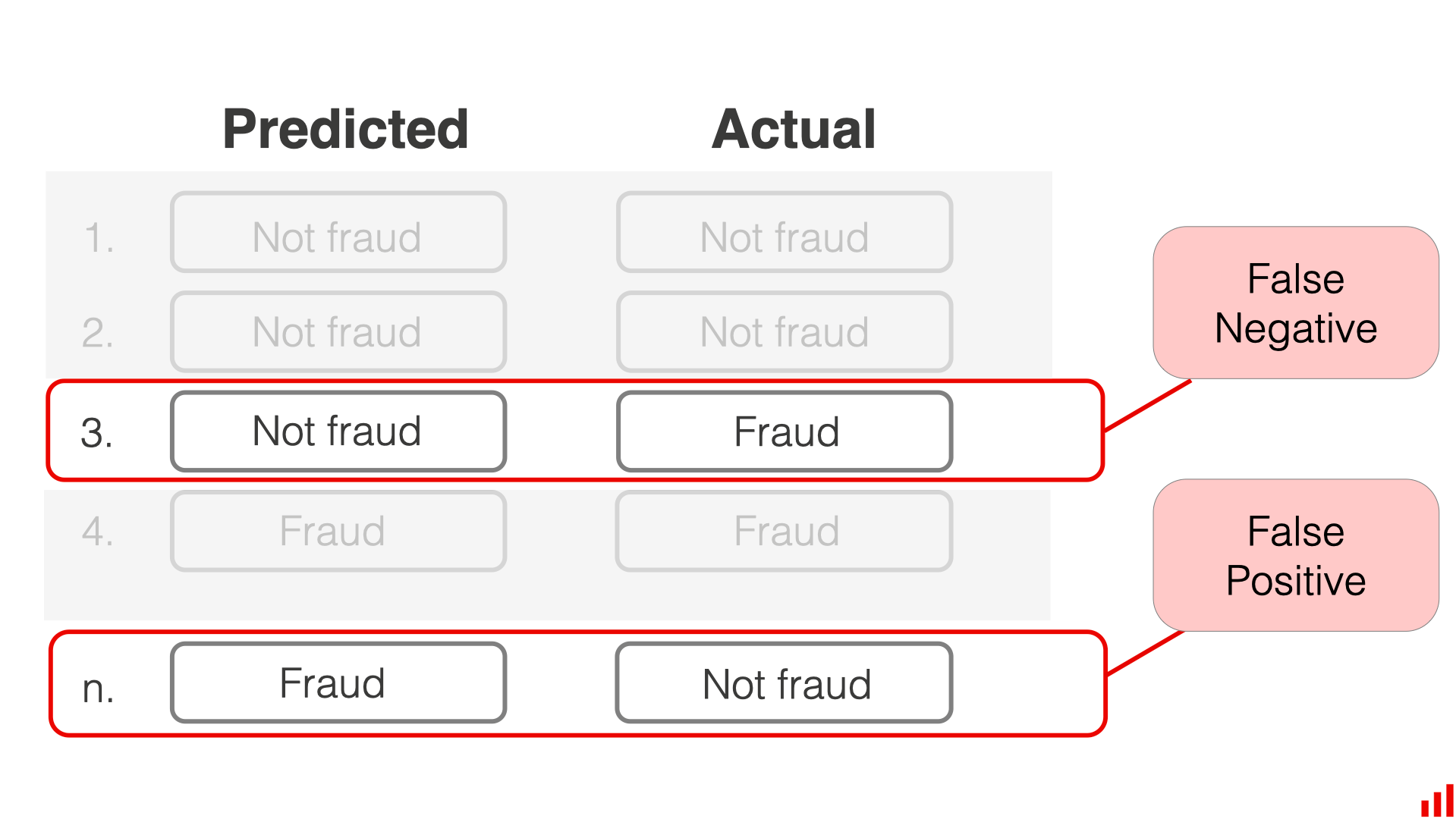
我想很多初学者,在刚接触到的时候,会对False Positive/False Negative 本身产生疑惑。
何为 FP,何为 FN?为什么将实际为普通的交易判定成为了欺诈交易,就定义为 FP,为啥不是 FN,识别错的了 negative 不可以吗?
其实这里的 False 和 True,是基于我们的模型目标,我们的模型期望是找出欺诈的交易,样本中的 Positive 就是欺诈样本
所以本身是正常的,判定为了欺诈(positive),那就是错误的 positive,所以就是 FP,FN 同理。
FP 和 FN 非常重要,所造成后果也不一样

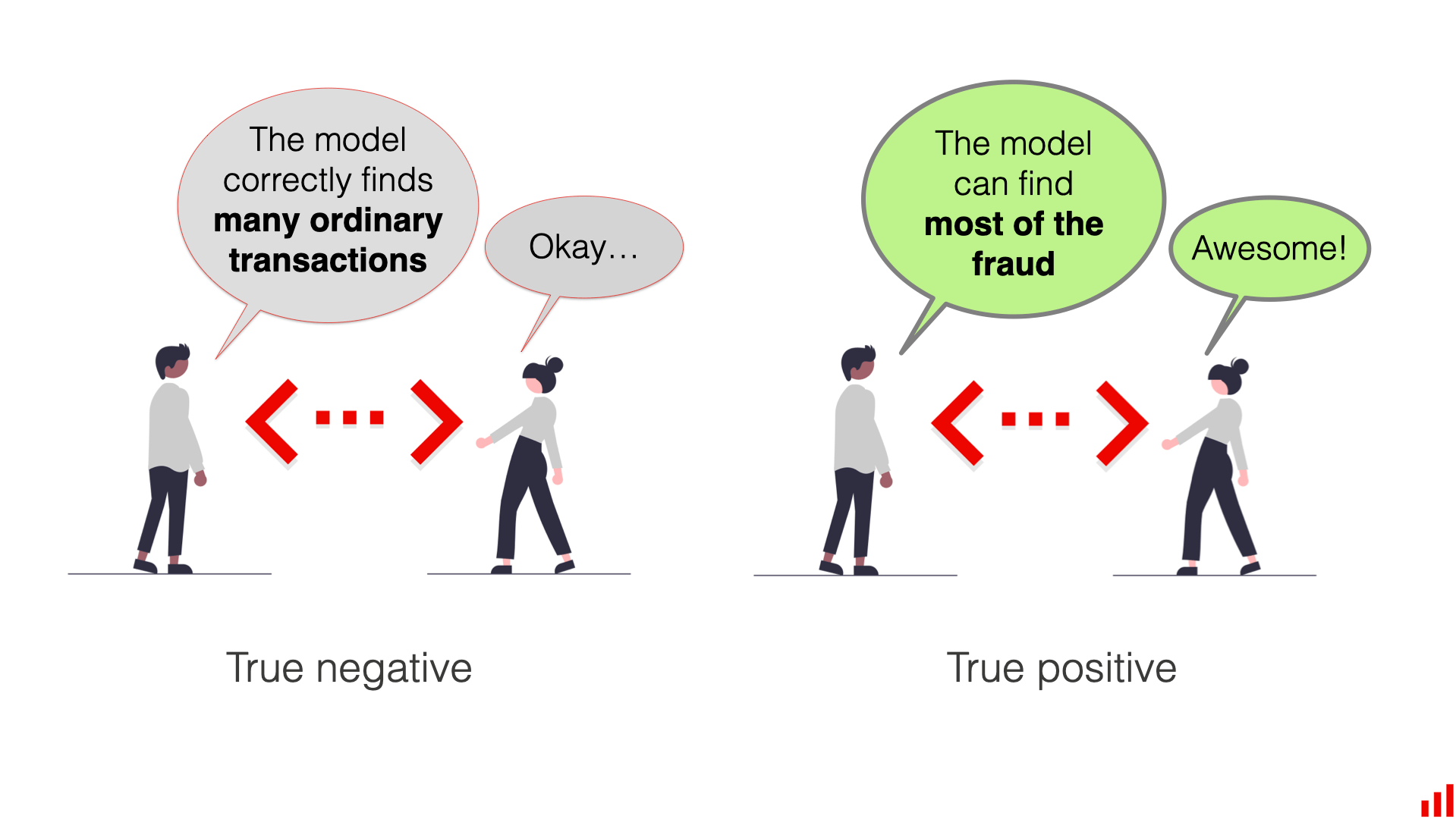
当然,TP 和 TN,应该不要花费过多时间去理解

当然,关注模型识别正确交易的能力也很重要
混淆矩阵
现在,有了 TP、TN、FP、FN 之后,就可以制作混淆矩阵了
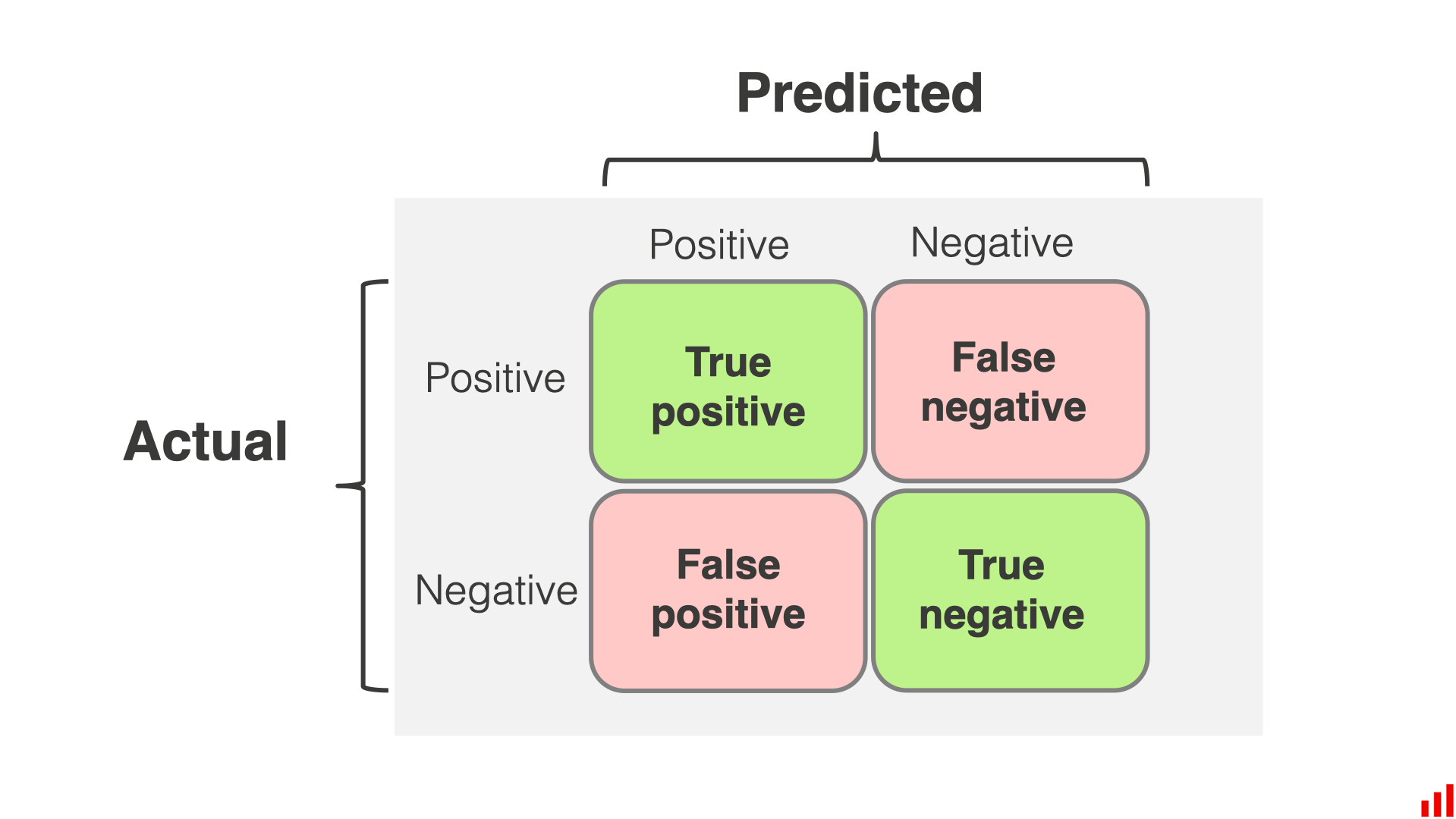
绘制并不难,一目明了,我并不想过多解释,关键是如何阅读?还是用一个垃圾邮件检测的模型来看
True Positive
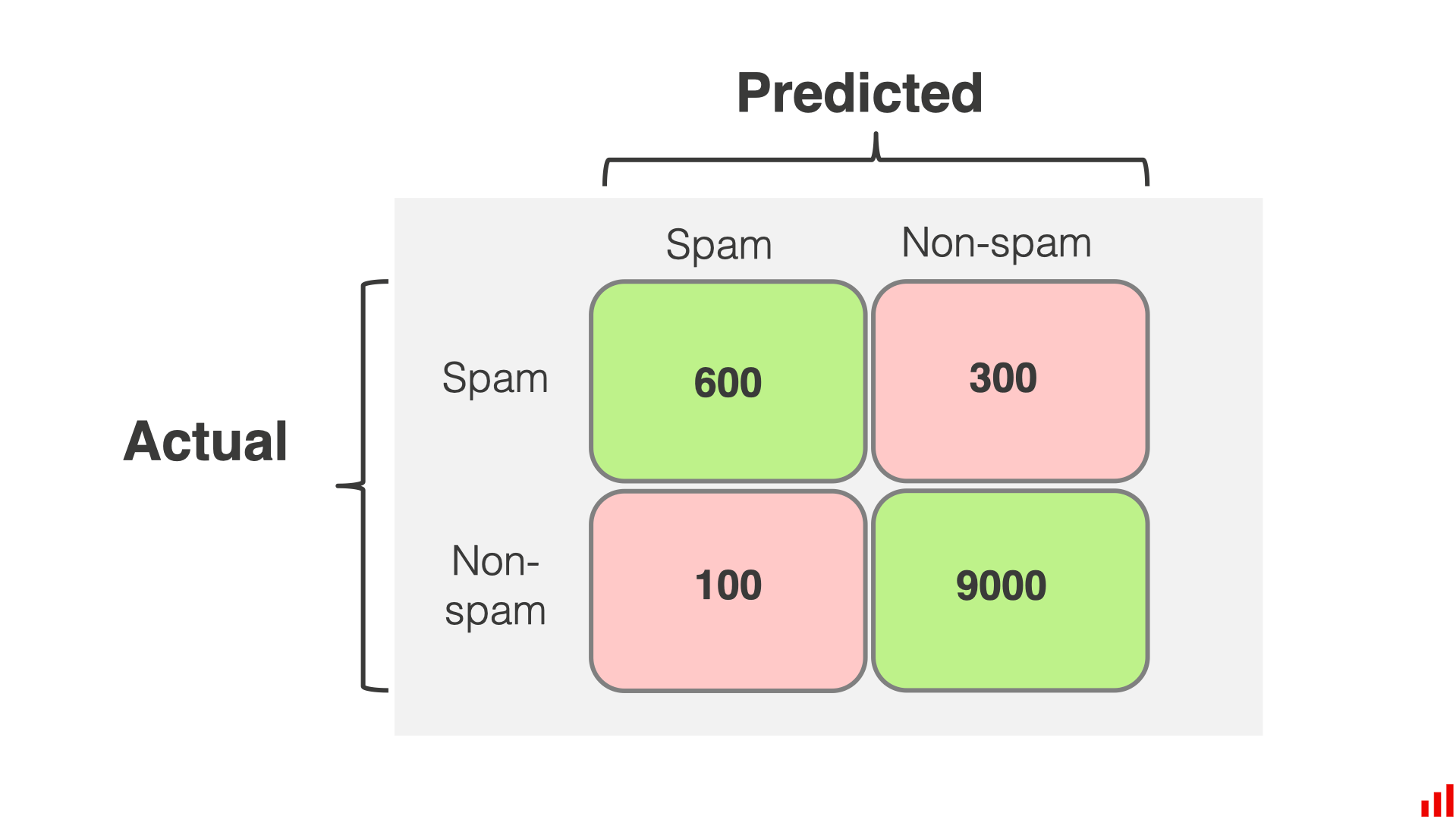
混淆矩阵的左上角,展示了该模型正确识别垃圾邮件的数量,在本例中,TP=600
True Negative
混淆矩阵的右下角,展示了该模型正确识别普通邮件的数量,在本例中,TN=9000
False Positive
混淆矩阵的左下角,展示了错误的预测垃圾邮件的数量,也就是将普通邮件预测成了垃圾邮件的数量,在本例中FP=100
False Negative
混淆矩阵的右上角,展示了错误的预测正常邮件的数量,也就是将垃圾邮件预测成了正常邮件的数量,在本例中,FN=300
基本评估指标
混淆矩阵只是展示了正确和错误预测的绝对数量,如果想进一步评估模型,就需要更多的指标,以下是常见的评估指标
Accuracy
准确率是指正确分类的样本占总样本的比例,差不多就是从整体上看,模型的效果
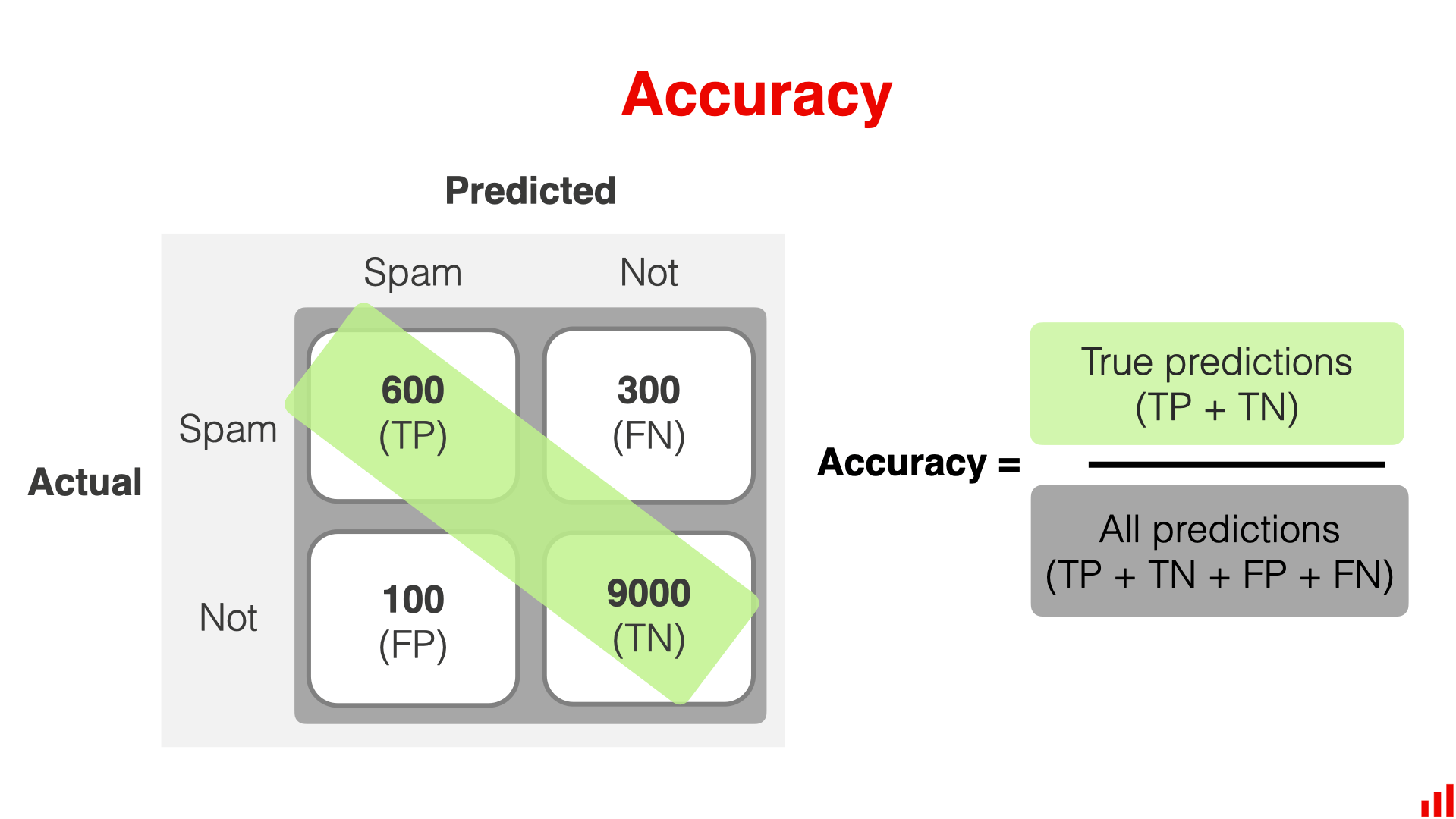
上面的例子中,准确率为 (9000+600)/10000 = 0.96。 模型在 96% 的情况下是正确的。
但是,对于不平衡的数据集来说,当某一类的样本明显较多时,准确率可能会产生误导。
在我们的例子中,有很多非垃圾邮件: 10000 封邮件中有 9100 封是正常邮件,也就是说即使将全部的邮件判定为正常邮件,准确率也会达到 91%
所以对于这个例子来说,整个模型的 Accuracy 仅反映了模型识别非垃圾邮件的能力。 如果对判定垃圾邮件感兴趣,那么仅看 accuracy 是不太够的。
Precision
Precision是预测的 positive 中有多少是真的 positive,也就是模型判断的垃圾邮件中,有多少是真的垃圾邮件
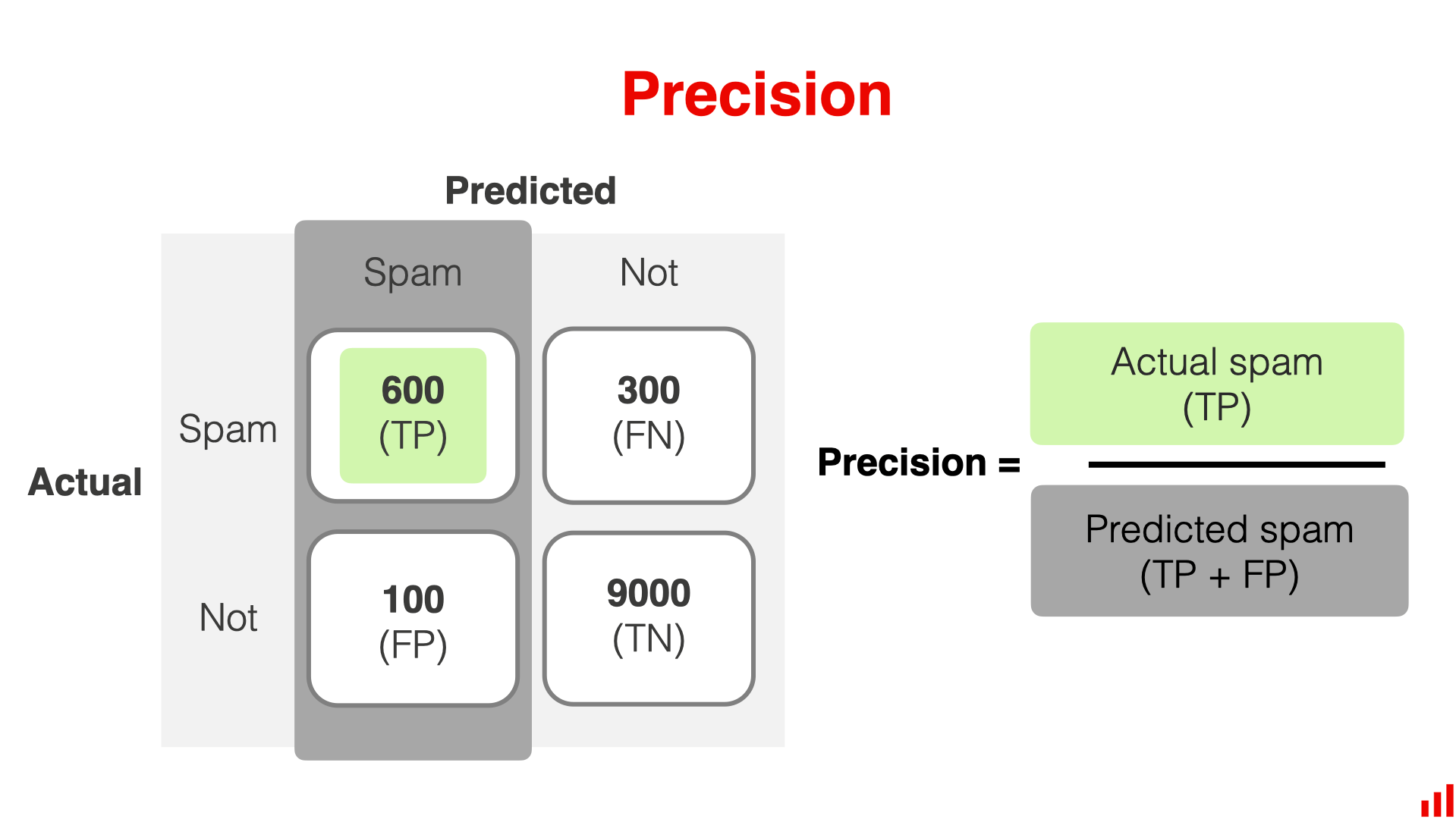
在上面的例子中,Precision是预测的为 600/(600+100)= 0.86。 在预测 "垃圾邮件 "时,该模型有 86% 的正确率
当FP成本较高时,精确度是一个很好的指标。 如果您希望避免将好的电子邮件发送到垃圾邮件文件夹,那么您可能希望将主要精力放在精确度上。
Recall
Recall(TPR)代表了,在真的positive 中,有多少被模型检测出来了
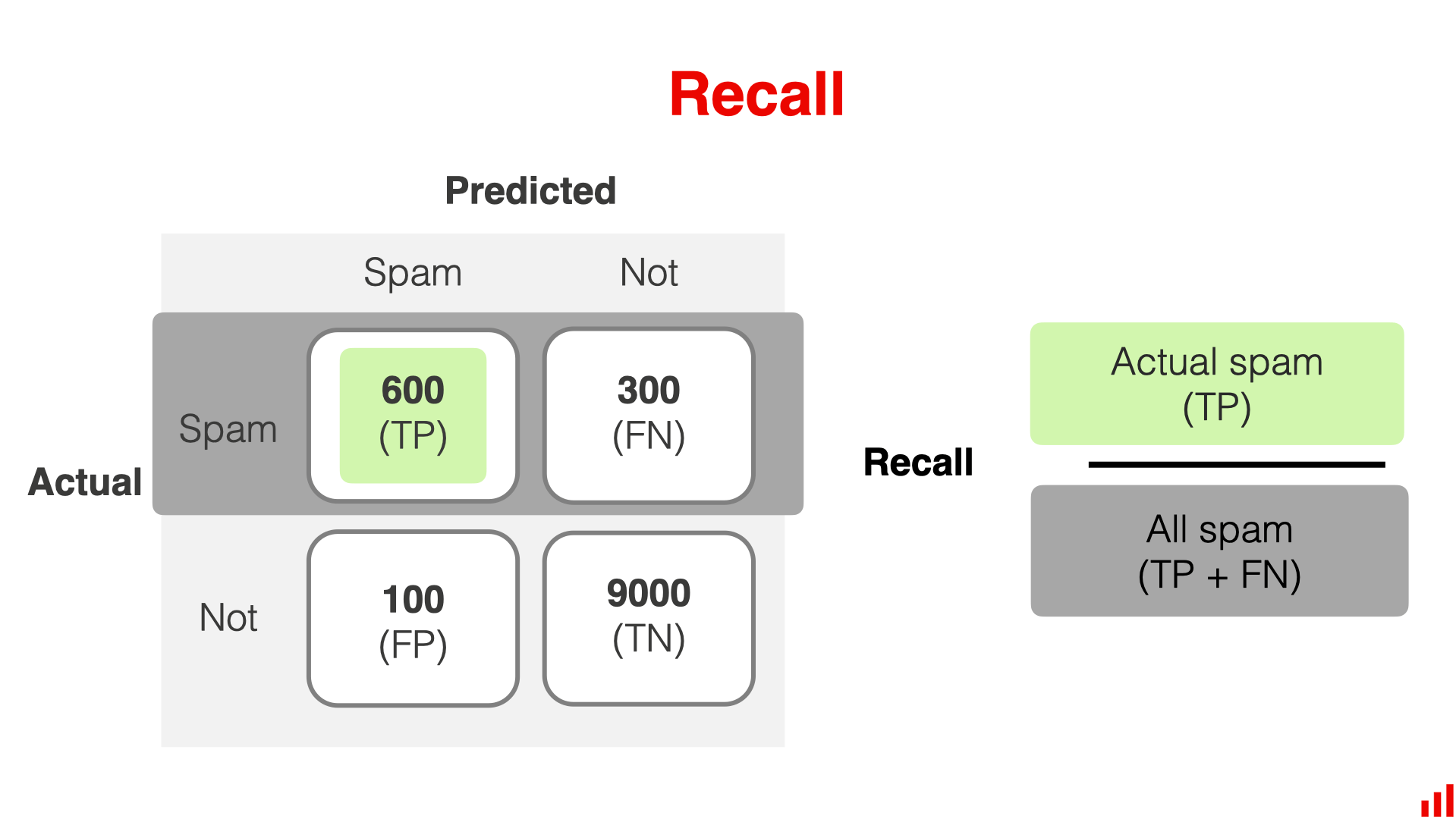
在上面的例子中,召回率为 600/(600+300)= 0.67。 该模型正确找到了 67% 的垃圾邮件。
当FN的代价很高时,召回率就是一个有用的指标。 例如,如果您不想漏掉任何垃圾邮件(甚至不惜错误标记一些合法邮件),就可以优化召回率。
参考链接
How to interpret a confusion matrix for a machine learning model