Skip to main content

Population stability index(PSI)

Population stability index(PSI)群体稳定性指标，常用来评估模型/特征的稳定性。

如何评估？

如果某个特征/模型分，对同一批的样本，在某个时间周期内分布是 A，另一个时间周期内，分布是 B，要是 A 和 B 的差异很大，那这个模型/特征肯定不会很好

如下图，哪个模型更好，一目了然

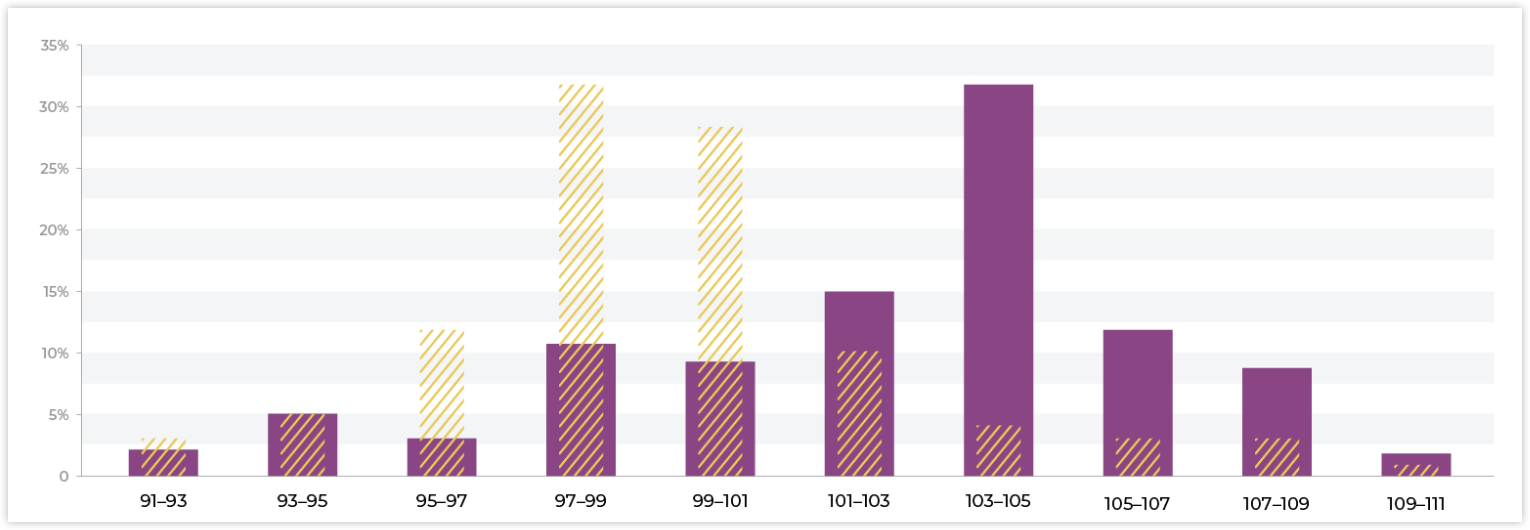
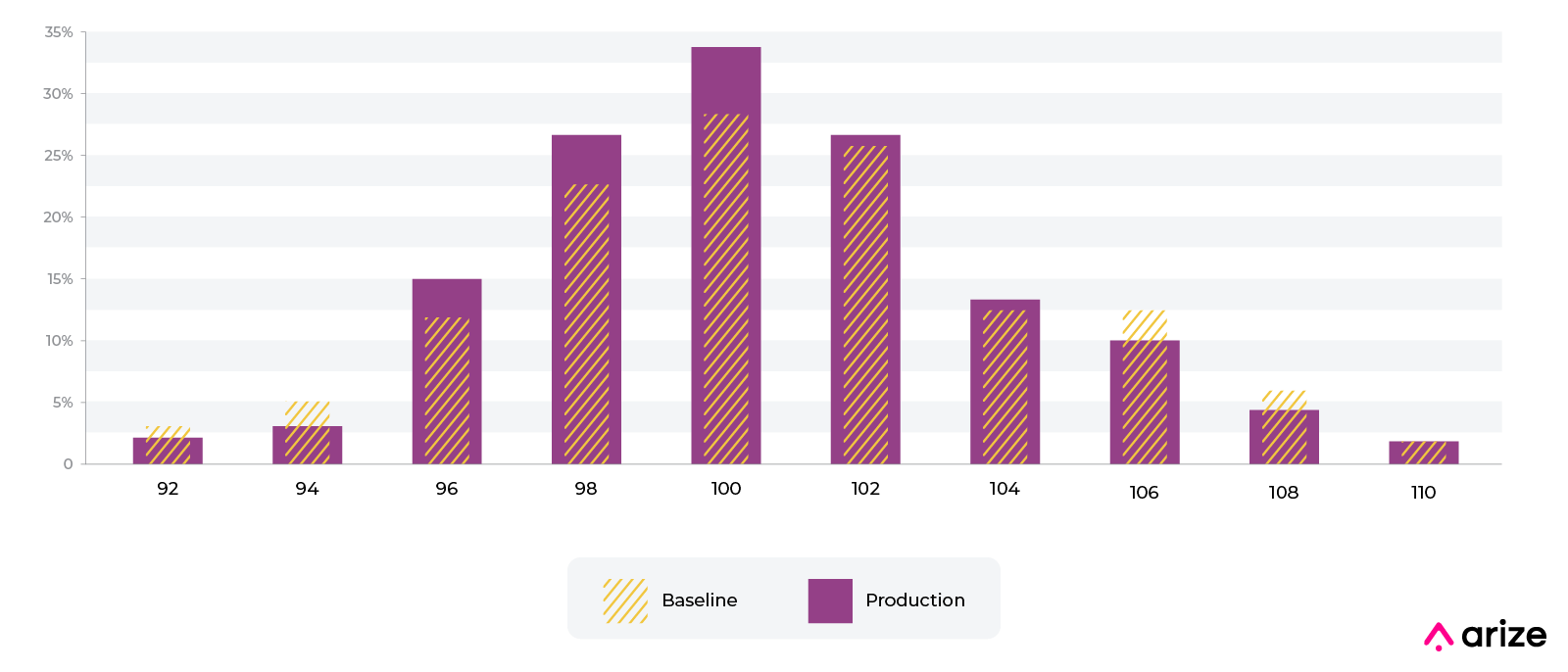
实际应用的话，比如说，在模型上线时候，前端流量有5000的测试用户，模型输出的分布可能是下面这样的。如果业务设置阈值为 60 分，那么，60 分以下的人我们会拒绝放款。这样一来，模型会拒绝掉大概 20%的人，这种情况对于业务来说是可以接受的。

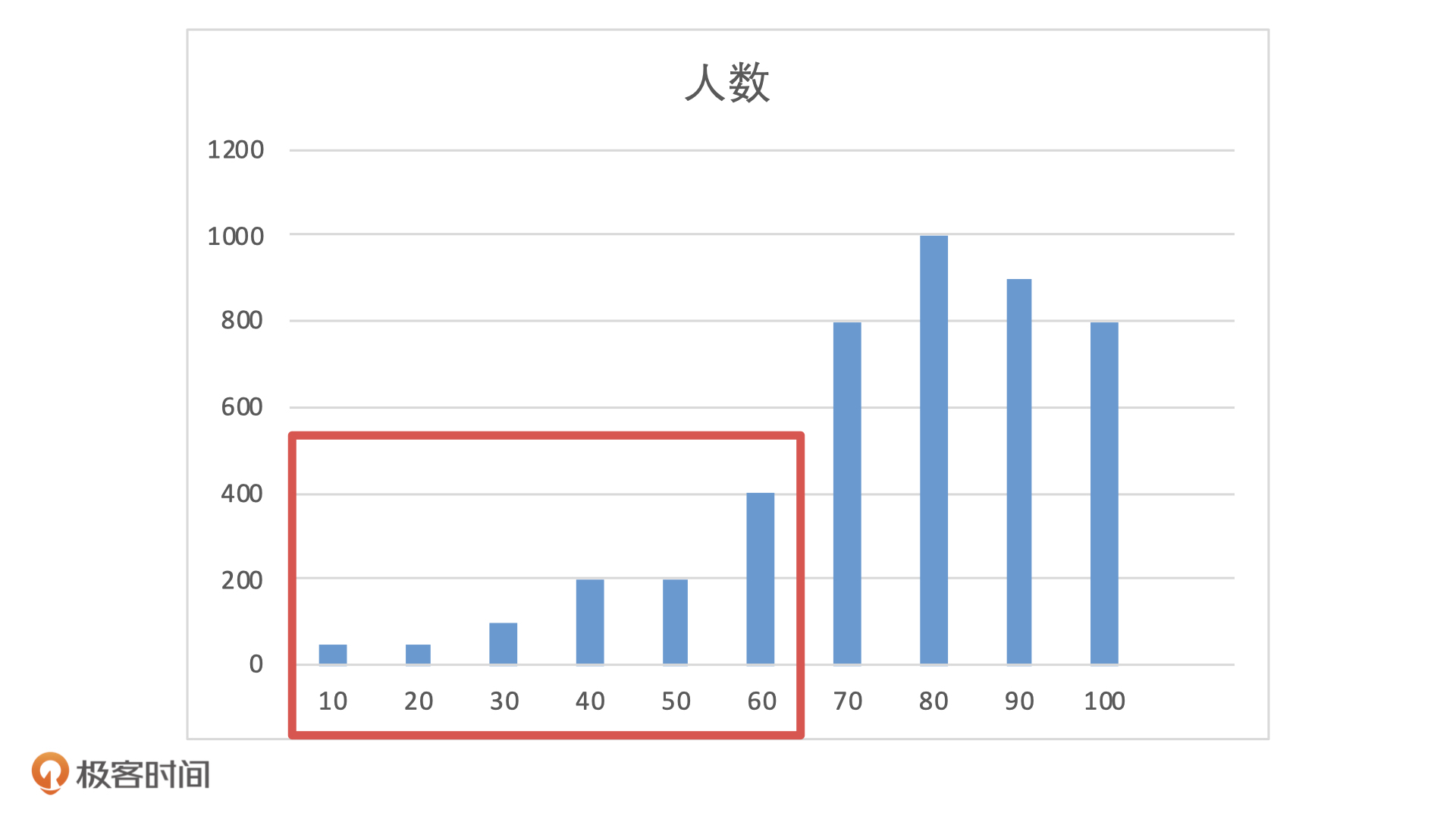
如果模型上线后，前端流量没有发生变化，还是 5000 个待测用户，但是客群发生了变化，从测试用户变成了线上的用户。这个时候，模型输出的分布就会变成下面这样。

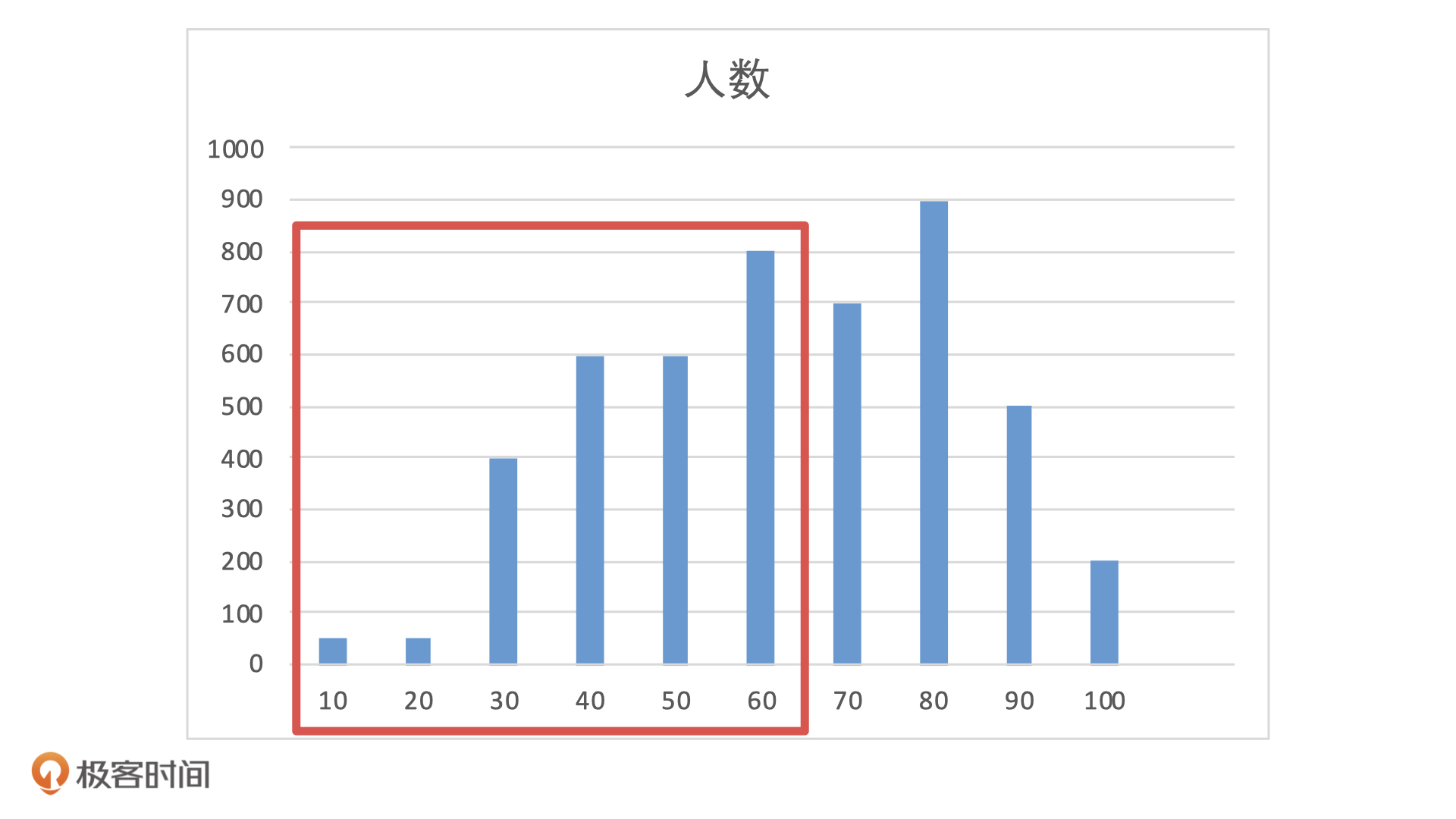
如果我们还是用 60 作为阈值，模型就会拒绝掉 50% 的用户。当前市场下，前端流量这么贵，如果风控拒绝了 50% 的用户申请，估计市场或者运营的同学，肯定不会放过风控部门了。

在实际工作中，这种情况的发生就是因为模型不稳定。为了避免这种情况的发生，我们必须要在上线前对模型的稳定性进行评估，尤其是在类似金融风控这类对模型稳定性要求高的场景中。

计算公式​

PSI 的计算公式比较简单，分箱 - 计算两组数据在每一箱的占比 - 按照如下公式计算最终的 psi

PSI=∑i=1n(Ai−Ei)×ln⁡(AiEi)\text{PSI} = \sum_{i=1}^{n} (\text{A}_i - \text{E}_i) \times \ln\left(\frac{\text{A}_i}{\text{E}_i}\right)

其中：

  • Ai\text{A}_i 是当前时间段包含样本的实际占比。
  • Ei\text{E}_i 是当前时间段包含样本的预期占比。
  • nn 是分箱的总数。

所以 PSI = SUM( (实际占比 - 预期占比） ln(实际占比 / 预期占比) )

计算步骤与例子​

一般来说，在机器学习建模的过程中，可以采用如下过程计算 PSI

  • step1：将变量预期分布（excepted）进行分箱（binning）离散化，统计各个分箱里的样本占比。
  • step2: 按相同分箱区间，对实际分布（actual）统计各分箱内的样本占比。
  • step3: 计算各分箱内的A - E和Ln(A / E)，计算index = (实际占比 - 预期占比）* ln(实际占比 / 预期占比) 。
  • step4: 将各分箱的index进行求和，即得到最终的PSI。

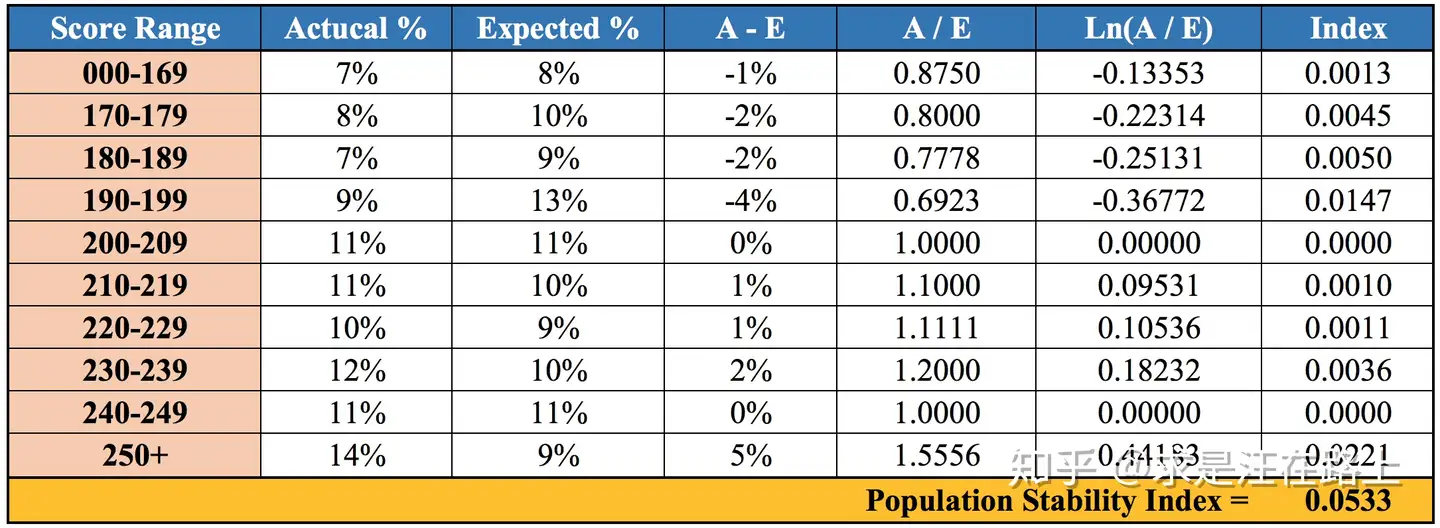
以下面的代码为例

# Development dataset
dev_data = pd.DataFrame({'score': [15, 20, 25, 30, 20, 15, 10, 5, 30, 10]})
# Validation dataset
val_data = pd.DataFrame({'score': [15, 20, 24, 25, 20, 15, 10, 5, 30, 10]})

首先对数据进行分箱

  • Bin 1: [0-9]
  • Bin 2: [10-19]
  • Bin 3: [20-29]
  • Bin 4: [30-39]
  • Bin 5: [40-49]

然后计算每一箱的占比，对于 dev 来说

  • Bin 1: 1/10 = 0.1
  • Bin 2: 3/10 = 0.3
  • Bin 3: 3/10 = 0.3
  • Bin 4: 2/10 = 0.2
  • Bin 5: 0/10 = 0

对于 Val 来说

  • Bin 1: 1/10 = 0.1
  • Bin 2: 3/10 = 0.3
  • Bin 3: 4/10 = 0.4
  • Bin 4: 1/10 = 0.1
  • Bin 5: 0/10 = 0

现在计算每一箱的 psi

  • Bin 1: (0.1 – 0.1) * ln(0.1 / 0.1) = 0
  • Bin 2: (0.3 – 0.3) * ln(0.3 / 0.3) = 0
  • Bin 3: (0.4 – 0.3) * ln(0.4 / 0.3) ≈ 0.111226
  • Bin 4: (0.1 – 0.2) * ln(0.1 / 0.2) ≈ 0.079441
  • Bin 5: Since both Dev% and Val% are 0, the PSI component is 0.

那么最终的 PSI 就是，当然这个数值在实际应用是一个不可以接受的值

PSI=0+0+0.111226+0.079441+0=0.190667PSI = 0 + 0 + 0.111226 + 0.079441 + 0 = 0.190667

评判标准​

一般来说，会要求 PSI 小于 0.1

  • PSI < 0.1：变化不显著 - 您的模型是稳定的！
  • 0.1 <= PSI < 0.25：中等变化——考虑一些调整。
  • PSI >= 0.25：重大变化——您的模型不稳定，需要更新

与 KL 散度（相对熵）关系​

转自 知乎

KL 散度​

相对熵（relative entropy），又被称为Kullback-Leibler散度（Kullback-Leibler divergence）或信息散度（information divergence），是两个概率分布间差异的非对称性度量。

划重点——KL散度不满足对称性。

我们先不考虑相对熵的计算逻辑，先看它的物理含义是什么？

相对熵可以衡量两个随机分布之间的”距离“，当两个随机分布相同时，它们的相对熵为零；当两个随机分布的差别增大时，它们的相对熵也会增大。

注意

相对熵是一个从信息论角度量化距离的指标，与数学概念上的距离有所差异。数学上的距离需要满足：非负性、对称性、同一性、传递性等；而相对熵不满足对称性。

看到这里，是不是感觉和PSI的概念非常相似？

当两个随机分布完全一样时，PSI = 0；反之，差异越大，PSI越大。

直觉告诉我们相对熵和PSI应该存在着某种隐含的关系，真相正在慢慢浮出水面。

我们再来看相对熵的计算公式。在信息理论中，相对熵等价于两个概率分布的信息熵（Shannon entropy）的差值。

KL(P∥Q)=−∑x∈XP(x)log⁡1P(x)+∑x∈XP(x)log⁡1Q(x))=∑x∈XP(x)log⁡P(x)Q(x)KL(P \| Q) = - \sum_{x \in X} P(x) \log \frac{1}{P(x)} + \sum_{x \in X} P(x) \log \frac{1}{Q(x)}) = \sum_{x \in X} P(x) \log \frac{P(x)}{Q(x)}

其中，P(x)表示数据的真实分布，而Q(x)表示数据的观察分布。上式可以理解为：

概率分布携带着信息，可以用信息熵来衡量。若用观察分布Q(x)来描述真实分布P(x)，还需要多少额外的信息量？

因此，KL散度是单向描述信息熵差异。

相对熵与PSI之间的关系​

接下来，我们从数学上来分析相对熵和PSI之间的关系。

psi=∑i=1n(Ai−Ei)×ln⁡(AiEi)psi=∑i=1nAi×ln⁡(AiEi)+∑i=1nEi×ln⁡(EiAi)\begin{array}{l} \text{psi} = \sum_{i=1}^n (A_i - E_i) \times \ln\left(\frac{A_i}{E_i}\right) \\ \\ \text{psi} = \sum_{i=1}^n A_i \times \ln\left(\frac{A_i}{E_i}\right) + \sum_{i=1}^n E_i \times \ln\left(\frac{E_i}{A_i}\right) \end{array}

将PSI计算公式变形后可以分解为2项，其中：

  • 第1项：实际分布（A）与预期分布（E）之间的KL散度 —— KL(A∥E)KL(A \| E)
  • 第2项：预期分布（E）与实际分布（A）之间的KL散度 —— KL(E∥A)KL(E \| A)

因此，PSI本质上是实际分布（A）与预期分布（E）的KL散度的一个对称化操作。

其双向计算相对熵，并把两部分相对熵相加，从而更为全面地描述两个分布的差异。

进一步理解​

在知乎看到如下回帖，感觉说的也挺有道理

主要讨论的点的是：PSI 大了，到底能不能说是模型不好？

我个人的看法是

从模型效果的角度来看，确实这个模型，已经不适用于当前的样本，但到底是因为模型建模的时候没有做好，还是客群本身质态就和建模样本发生了偏移，这很难说

Last updated on by lzq_dxm