WOE 和 IV

WOE - Weight of Evidence

WOE（Weight of Evidence）即证据权重，是对原始自变量的一种编码形式

WOE可以理解为“当前分组中响应客户占样本所有响应用户的比例”和“当前分组中没有响应的客户占样本中所有没有响应的比例”的差异性。WOE越大，这种差异越大，这个分组里的样本响应的可能性就越大，WOE越小，差异越小，这个分组里的样本响应的可能性就越小。

理解一下WOE，会发现，WOE其实描述了变量当前这个分组，对判断个体是否会响应（或者说属于哪个类）所起到影响方向和大小，当WOE为正时，变量当前取值对判断个体是否会响应起到的正向的影响，当WOE为负时，起到了负向影响。而WOE值的大小，则是这个影响的大小的体现

计算公式的深入理解

来自知乎：风控模型—WOE与IV指标的深入理解应用

首先给出 WOE 的一般公式定义

$$\begin{equation} W O E_i=\ln \left(\frac{\text { Bad }_i}{\text { Bad }_T} / \frac{\text { Good }_i}{\text { Good }_T}\right)=\ln \left(\frac{\text { Bad }_i}{\text { Bad }_T}\right)-\ln \left(\frac{\text { Good }_i}{\text { Good }_T}\right) \end{equation}$$

WOE = ln (第i个分箱的坏人数 / 总坏人数) - ln (第i个分箱的好人数 / 总好人数)

此时可以理解为：每个分箱里的坏人分布相对于好人分布之间的差异性，我们对公式再变换为：

$$\begin{equation} W O E_i=\ln \left(\frac{\text { Bad }_i}{\text { Bad }_T} / \frac{\text { Good }_i}{\text { Good }_T}\right)=\ln \left(\frac{\text { Bad }_i}{\text { Good }_i}\right)-\ln \left(\frac{\text { Bad }_T}{\text { Good }_T}\right) \end{equation}$$

WOE = ln (第i个分箱的坏人数 / 第i个分箱的好人数) - ln (总坏人数 / 总好人数)

此时可以理解为：每个分箱里的坏好比(Odds)相对于总体的坏好比之间的差异性。

但是，为什么要再套一个对数ln？

之前看到一种解释是为了进行平滑处理。那么为什么不引入拉普拉斯平滑，也就是在分子分母中都加上一个数？如果加上1，那么公式推导如下：

$$\begin{equation} \begin{align*} & \left(\frac{\text{Bad}_i}{\text{Good}_i}+1\right) /\left(\frac{\text{Bad}_T}{\text{Good}_T}+1\right) \\ & =\left(\frac{\text{Bad}_i+\text{Good}_i}{\text{Good}_i}\right) /\left(\frac{\text{Bad}_T+\text{Good}_T}{\text{Good}_T}\right) \\ & =\text{Good\_Rate}_T / \text{Good\_Rate}_i \end{align*} \end{equation}$$

此时含义是：总体good_rate相对于分箱内good_rate的倍数。

其实发现这种形式会更符合我们的直觉。因此，“取对数是为了平滑处理”——这种解释无法说服我们。

从贝叶斯角度理解WOE

贝叶斯理论认为我们认知世界是一个循序渐进的过程，首先我们有一个主观的先验认知，进而不断通过观测数据来修正先验认知，得到后验认知。随着这个过程不断迭代，我们对世界的认识也就越来越完善。其中，从观测数据中提取信息来支撑我们的原始假设就是WOE。

在信贷风控中，识别好人和坏人也是同样的道理。我们根据历史样本数据形成一个先验认知：

$$\begin{equation} \begin{aligned} & \left\{\begin{aligned} P(\text { Bad }) & =\frac{\text { Bad }_T}{\text { Good }_T+\text { Bad }_T} \\ P(\text { Good }) & =\frac{\text { Good }_T}{\text { Good }_T+\text { Bad }_T} \end{aligned}\right. \\ & =>\text { Odds }=\frac{P(\text { Bad })}{P(\text { Good })}=\frac{\text { Bad }_T}{\text { Good }_T} \\ & \end{aligned} \end{equation}$$

当Odds小于1时，预测为Good的概率更高，此时我们认为一般情况下都是好人。但实际中样本会受到各种因素（自变量）影响而导致变坏。

因此，我们就开始搜集样本的各种特征，希望这些证据能帮助我们对这个样本全貌有更为全面的理解，进而修正我们的先验认识。这个过程用公式可以表达如下。

提示：留意两侧为什么会取自然对数ln，而不是log？

$$\begin{equation} \begin{aligned} & \left\{\begin{array}{r} p(Y=B a d \mid X)=\frac{p(X \mid Y=B a d) p(Y=B a d)}{P(X)} \\ p(Y=G o o d \mid X)=\frac{p(X \mid Y=G o o d) p(Y=\text { Good })}{P(X)} \end{array}\right. \\ & \Rightarrow \frac{p(Y=B a d \mid X)}{p(Y=\text { Good } \mid X)}=\frac{p(X \mid Y=\text { Bad }) p(Y=B a d)}{p(X \mid Y=\text { Good }) p(Y=\text { Good })} \\ & \Rightarrow \ln \left(\frac{p(Y=B a d \mid X)}{p(Y=\text { Good } \mid X)}\right)=\ln \left(\frac{p(X \mid Y=\text { Bad })}{p(X \mid Y=\text { Good })}\right)+\ln \left(\frac{p(Y=B a d)}{p(Y=\text { Good })}\right) \\ & \Rightarrow \ln \left(\frac{B a d}{\text { Good }}\right)=W O E+\ln \left(\frac{\text { Bad }_T}{\text { Good }_T}\right) \\ & \Rightarrow W O E=\ln \left(\frac{B a d}{\text { Good }}\right)-\ln \left(\frac{\text { Bad }_T}{\text { Good }_T}\right) \\ & \end{aligned} \end{equation}$$

其中, $\ln \left(\frac{p(Y=B a d \mid X)}{p(Y=\operatorname{Good} \mid X)}\right)$ 表示后验项; $\ln \left(\frac{p(X \mid Y=B a d)}{p(X \mid Y=G o o d)}\right)$ 表示根据观测数据更新信息，即 WOE; $\ln \left(\frac{p(Y=B a d)}{p(Y=G o o d)}\right)$ 表示先验项。

如果搜集到的数据与先验认知的差距不大，我们就认为这个数据中得到的证据价值不大，反之则认为带来的信息越多。因此，WOE用以衡量对先验认识修正的增量，这就是WOE被取名为“证据权重”的原因。

一个例子

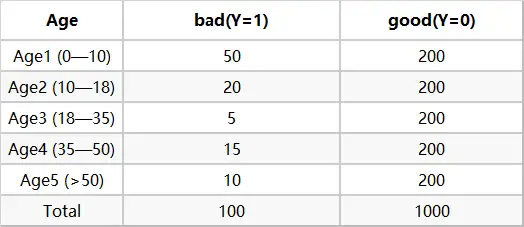
最后举一个计算 WOE 的例子，以信用评分卡的建模场景为例：$X$是客户样本字段，$Y$表示客户逾期与否，其中$Y=1$代表逾期，$Y=0$代表未逾期。

我们希望能用客户已知的信息来预测客户借款后发生逾期的概率，以此来决定是否放贷。

下面我们拿Age(年龄)这个变量来计算相关的woe ，首先对每个level分层统计

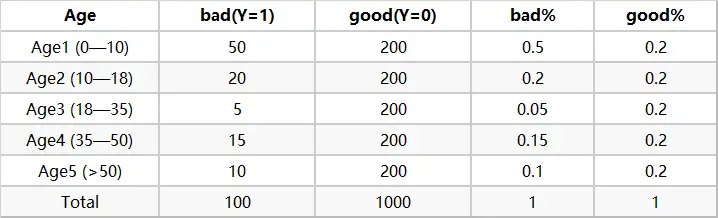
然后计算各分层的好坏占比

最后通过好坏占比计算WOE

当我们算完WOE的时候，我们一般会关注 WOE 是否单调，WHY ？

首先 WOE 要分箱后箱之间保持单调，是为了对分箱过程的约束（避免分箱过程太过贴近样本，即过拟合，避免波浪形分箱的存在）

其次为了确保业务上的可解释性（随着业务变量增大，用户为好用户概率也随着业务量单调变化），由于目的是为了可解释性，那么一些业务上课解释的变量，U型时也是可以的，比如说大家提到的年龄变量

回到上面的例子，WOE单调实际上就意味着当 $A g e_i$ 从 $A g e_1 \rightarrow A g e_2 \rightarrow A g e_3 \rightarrow A g e_4 \rightarrow A g e_5$ 单调上升时, 相应的bad rate越低，这时通过WOE变换，特征值不仅仅代表一个分类，还代表了这个分类的权重！

IV

IV的全称是Information Value，中文意思是信息价值，或者信息量。

我们在用逻辑回归、决策树等模型方法构建分类模型时，经常需要对自变量进行筛选。比如我们有200个候选自变量，通常情况下，不会直接把200个变量直接放到模型中去进行拟合训练，而是会用一些方法，从这200个自变量中挑选一些出来，放进模型，形成入模变量列表。那么我们怎么去挑选入模变量呢？

挑选入模变量过程是个比较复杂的过程，需要考虑的因素很多，比如：变量的预测能力，变量之间的相关性，变量的简单性（容易生成和使用），变量的强壮性（不容易被绕过），变量在业务上的可解释性（被挑战时可以解释的通）等等。但是，其中最主要和最直接的衡量标准是变量的预测能力。

“变量的预测能力”这个说法很笼统，很主观，非量化，在筛选变量的时候我们总不能说：“我觉得这个变量预测能力很强，所以他要进入模型”吧？我们需要一些具体的量化指标来衡量每自变量的预测能力，并根据这些量化指标的大小，来确定哪些变量进入模型。IV就是这样一种指标，他可以用来衡量自变量的预测能力。类似的指标还有信息增益、基尼系数等等。

计算方法

IV值的计算依赖于WOE，可以看成对WOE的加权求和

$$\begin{equation} \begin{gathered} I V_i=\left(\frac{\text { Bad }_i}{\text { Bad }_T}-\frac{\text { Good }_i}{\text { Good }_T}\right) * \text { WOE }_i \\ =\left(\frac{\text { Bad }_i}{\text { Bad }_T}-\frac{\text { Good }_i}{\text { Good }_T}\right) * \ln \left(\frac{\text { Bad }_i}{\text { Bad }_T} / \frac{\text { Good }_i}{\text { Good }_T}\right) \\ I V=\sum_{i=1}^n I V_i \end{gathered} \end{equation}$$

IV值的范围是 $[0,+\infty)$, 当前分组中只包含响应客户或者未响应客户时, $I V=+\infty$

计算步骤

1. 对于连续型变量，进行分箱（binning），可以选择等频、等距，或者自定义间隔；对于离散型变量，如果分箱太多，则进行分箱合并。
2. 统计每个分箱里的好人数(bin_goods)和坏人数(bin_bads)。
3. 分别除以总的好人数(total_goods)和坏人数(total_bads)，得到每个分箱内的边际好人占比(margin_good_rate)和边际坏人占比(margin_bad_rate)。
4. 计算每个分箱里的 $WOE=\ln (\frac{\text { margin\_badrate }}{\text {margin\_goodrate}})$
5. 检查每个分箱（除null分箱外）里woe值是否满足单调性，若不满足，返回step1。注意：null分箱由于有明确的业务解释，因此不需要考虑满足单调性。
6. 计算每个分箱里的IV，最终求和，即得到最终的IV。

为什么用IV而不是直接用WOE？

• 当我们衡量一个变量的预测能力时，我们所使用的指标值不应该是负数
• IV在WOE的前面乘以了一个系数，而这个系数很好的考虑了这个分组中样本占整体样本的比例，比例越低，这个分组对变量整体预测能力的贡献越低。相反，如果直接用WOE的绝对值加和，会得到一个很高的指标，这是不合理的

最后引用一段话来说明两者之间的关系

1. WOE describes the relationship between a predictive variable and a binary target variable.
2. IV measures the strength of that relationship.

参考文章

1. 风控模型—WOE与IV指标的深入理解应用
2. 【详解】银行信用评分卡中的WOE在干什么？
3. WOE编码为啥有效